To solve a triangle, three facts about it must be supplied. At least one of these items of information must be the length of one of the sides. The other two items must each be either the length of a side or the magnitude of an angle.

Using this information, UltimaCalc will calculate, if this is possible, the remaining sides or angles, and also the triangle's area and perimeter.

UltimaCalc shows the triangle graphically, always with one of the sides horizontal. The displayed triangle can be rotated, or shown as a mirror image, or inverted vertically.

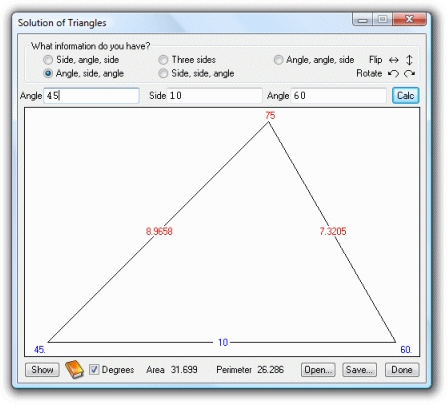
In the image above, the values that were entered (the given values) are shown in blue and the calculated values are shown in red. The triangle has been drawn to scale. If a side, or one or two angles, are so small that a scale drawing is undesirable, a warning will be shown, and the triangle will be drawn as closely as possible to its actual shape.

The button marked 'Show' will display all the sides, angles, area and perimeter in a multiple results window, from which all this information can be copied to the Windows clipboard. The information can then be pasted into any word or text processor.

Next to this button is a graphical representation of a log book. Clicking on this when it is highlighted will cause the calculation and its results to be recorded to a log file.

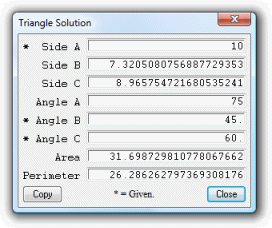
The supplied data, along with information about how the triangle is to be displayed, can be saved as a plain text file for future reference.

The given and calculated values are also stored as variables in the main calculator. While the triangles window is open, the main calculator window can continue to be used as normal.

Because UltimaCalc understands algebraic expressions, the data you enter need not consist of only purely numerical values. For example, when calculating in radians you can enter angles as fractions of pi.

Another example: calculate a triangle given three sides, with the first one specified as p = 5, the second side as p - 1, and the third side as sqrt(2*p - 1). UltimaCalc will show a right-angled triangle. If the value specified for the first side is changed, provided that it is greater than 1, you get a different right-angled triangle. For example, try changing the first side to p = 13.

If we know some of the properties of a triangle, how do we calculate its other properties? To define a triangle, we need to specify three independent facts about it. Each of these facts can be the length of some other side, or an angle, or the perimeter of the triangle, or its area.

Notice that the previous statement implies that it is not sufficient to specify only the three angles. The sum of the angles of a triangle is always the same, 180 degrees, so having specified two of the angles, the third angle is easily calculated and is clearly not an independent fact.

Let's draw a triangle and see if we can find some kind of relationship between its sides and its angles. We'll call the vertexes (or the angles) A, B and C, and we'll call the lengths of the sides opposite these vertexes a, b and c.

To give us something to play with, I have drawn a line representing the height of the triangle. This line splits the original triangle into two right-angled triangles.

Elementary trigonometry now gives us the following relationships:

sin(A) = h / b  and  sin(B) = h / a

We don't want to get involved with what the value of h might be, so let's combine these two equations so as to eliminate h. The most easily remembered equation that we get from doing this is:

a / sin(A) = b / sin(B)

This has been named the sine rule. By renaming the angles and sides (or by making another side the base of the triangle and drawing a new line for its height), we obtain the full version of the sine rule equation:

a / sin(A) = b / sin(B) = c / sin(C)

What can we do with this equation? Well, given two sides and the angle opposite one of these sides, we can calculate the angle opposite the other known side. Having done this, we then know two of the angles of the triangle, so we can calculate the remaining angle. Using the sine rule equation a second time, we can find the length of the side opposite this third angle.

Also, if we start by knowing any two of the angles, we can calculate the third angle. Then, if we know the length of one of the sides, we can use this equation to calculate the lengths of the other two sides.

Earlier, we decided to not get involved with the calculation of h, the height of the triangle. However, this is easy enough: the area of a triangle is half the product of its height and base. So h = 2 * area / c.

The simple sine rule equation has turned out to be a powerful tool. However, it is not the only tool we need. What if we have specified the three sides of a triangle? How do we calculate its angles? The sine rule does not seem to help here.

Let's go back to our triangle with its height drawn in. I stated earlier that the height line divides the triangle into two right angled triangles. Perhaps Pythagoras's theorem will help us find another useful rule.

I have labelled the foot of the height line D. Let x be the length of the line AD. For the new triangle ACD, Pythagoras's theorem states that h2 + x2 = b2. This doesn't look too useful. However, let's carry on, and apply Pythagoras to the other right-angled triangle. The distance BD is c-x and h2 + (c-x)2 = a2.

Comparing these two equations, we notice that we can easily combine them so as to get rid of h2. The resulting equation can be written as

a2 = b2 + c2 - 2 * c * x.

Can we also get rid of x ? Elementary trigonometry shows that x = b * cos(A). Substituting this into the previous equation gives:

a2 = b2 + c2 - 2 * b * c * cos(A)

This is called the cosine rule. If you look carefully at the symmetry of this equation, this will help you to remember it.

Earlier, we considered how we might solve a triangle given the lengths of its three sides. The cosine rule clearly does the job for us. It also works when we know two sides and the angle between them.

We have assumed up to this point that we can specify a combination of line lengths, angles, a perimeter or an area, and find the corresponding triangle. But the triangle might not actually exist! Simple examples are: (1) a triangle quoted as having one side longer than the sum of the other two sides; (2) two angles being given, but their sum exceeds 180 degrees; (3) quoting an area and perimeter, with the area being greater than the perimeter can possibly contain.

There is a gotcha with the sine rule, when calculating an angle. Given the sine of an angle, the angle may be less than or greater than 90 degrees. The sine of 80 degrees is the same as the sine of 100 degrees, for example, so you need to bear this kind of thing in mind and choose the appropriate angle. A sketch of the triangle can help here.

And then there is the question of a triangle specified by two sides and an angle opposite one of the known sides. For example, knowing the sides c and a and the angle A in the diagram above. The diagram indicates that two valid solutions are possible, as there are two possible locations for the side of length aa. Moreover, if a is less than the distance d, there is no possible solution.

When the triangle is specified by its area, its perimeter, and one angle, it is not obvious how to find its sides and other angles. We need to resort to some algebra.

The perimeter is the sum of the sides, so a = p-b-c where p is the perimeter.

The area is half the base times the height of the triangle. This gives the formula b = 2 * area/(c*sin(A)).

Use the first equation to remove a from the cosine rule, a2=b2+c2-2*b*c*cos(A), then use the second equation to remove b from the result. After tidying up the resulting expression, we obtain the following quadratic equation for the length c:

c2*2*p*sin(A) - c*(4*area*(1+cos(A))+p2*sin(A)) + 4*area*p = 0

Unfortunately, this is an instantly forgettable equation. This is probably why it does not seem to be published very often. However, it does work! Solving this quadratic will give us the lengths of the two sides adjacent to the given angle A. We can subtract these two sides from the perimeter to obtain the third side, a. We can now use the sine rule to calculate the remaining angles. It is a good idea to check that these angles do indeed add up to 180 degrees.

The equation in the previous section does not seem to be useful when we are given a side and want to know the angle. This is because the equation includes both the sine and the cosine of the angle. Let's use the identity sin(x)2+cos(x)2=1 to get rid of the sine term. The resulting equation is not at all nice, so I won't show it here.

To make the equation look simpler, I have defined q = (p*(p-2*c)/(4*area))2. With this definition, we now have a quadratic equation for cos(A), namely:

cos(A)2*c2*(q+1) - cos(A)*2*c*(p-c) + (p-c)2-c2*q = 0

So, knowing the area of a triangle, its perimeter, and one line, the equation can be solved for cos(A) and the two results will be the cosines of the two angles adjacent to the known line.

As an example, try a perimeter of 54, an area of 126, and a side length of 20. The two values of cos(A) are 0.8 and about 0.246154. You can verify that these two values are correct if I tell you that the perimeter and area were calculated for a triangle whose sides are 13, 20, and 21. In this triangle, the three angles have cosines of 16/20 = 0.8, 5/13 = 0.384615 and 16/65 = 0.246154.

These two equations using the area and perimeter are so instantly forgettable that it is no surprise that they are rarely published. On the other hand, the equations for the sine rule and the cosine rule are well known and easily memorised.

UltimaCalc has a tool for solving triangles. Unfortunately, in the current version it only knows the sine rule and the cosine rule, so it can only handle the cases where the angles and sides are known, and does not help directly when you only know the area and perimeter. However, you can still use UltimaCalc to quickly calculate the roots of the two quadratics.